maximos y minimos derivadas carolina santiago bautista

 

Máximos y mínimos relativos con el criterio de primera derivada

    Una función   f(x)   tiene un máximo relativo en   x = c   si   f(a) ≥ f(x)   para todo   x   en algún entorno del punto   a.

    Una función   f(x)   tiene un mínimo relativo  en   x = a   si   f(a) ≤ f(x)   para todo   x   en algún entorno del punto   a .

Criterio de la primera derivada

En un punto crítico   x = a ,  una función derivable   f(x)   tiene:

•   un máximo relativo si   f ' (x)   cambia de positiva a negativa (↑↓) 

•   un mínimo relativo si   f ' (x)   cambia de negativa a positiva (↓↑)

•   no tiene máximo ni mínimo relativo si   f ' (x)   no cambia de signo (↑↑  o  ↓↓)

Criterio de la segunda derivada

En un punto crítico   x = a ,  una función derivable   f(x)   tiene:

•   un máximo relativo si   f '' (a) < 0

•   un mínimo relativo si   f '' (a) > 0

EJEMPLOS DE CÁLCULO DE MÁXIMOS Y MÍNIMOS RELATIVOS CON EL CRITERIO DE LA PRIMERA DERIVADa y segunda derivada

Estudia los máximos y mínimos relativos de la siguiente función:

  f(x) = x³ - 3x + 2

1)   Se calcula la primera derivada:   f ' (x)

Calculamos la primera derivada de la función.

f ' (x) = 3x² - 3

2)   Se resuelve la ecuación:   f ' (x) = 0

A continuación calculamos las raíces de la primera derivada.

3x² - 3 = 0   ⇔   3x² = 3   ⇔   x² = 1   ⇔   x = ±1

Por lo tanto la primera derivada se anula en   x = -1   y   x = 1 .

3)   Se sustituyen las raíces de   f ' (x) = 0   en la función inicial y se obtienen los posibles máximos y mínimos relativos.

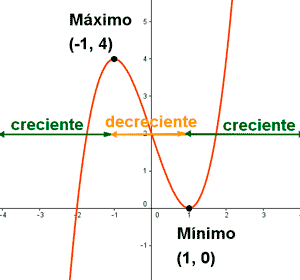
     •   f (-1) = 4   ⇒   El punto   (-1, 4)   es un posible máximo o mínimo relativo

     •   f (+1) = 0   ⇒   El punto   (+1, 0)   es un posible máximo o mínimo relativo

4)   Se calcula la segunda derivada:   f '' (x)

Calculamos la segunda derivada.

f '' (x) = 6x

5)   Se sustituyen la abscisa de los posibles máximos y mínimos relativos en la segunda derivada   f '' (x)

     •   Si   f '' (x) < 0   es un máximo relativo

     •   Si   f '' (x) > 0   es un mínimo relativo

En nuestro caso tenemos que:

     •   f '' (-1) = - 6 < 0   ⇒   (-1, 4)   es un máximo relativo

     •   f '' (+1) = 6 > 0   ⇒   (+1, 0)   es un mínimo relativo

                          Puntos de inflexión.

Un punto de inflexión, en una función matemática, es un punto donde los valores de una función continua en x pasan de un tipo de concavidad a otra. La curva "atraviesa" la tangente.

El punto de inflexión de una función matemática es aquel punto en el que la gráfica que la representa cambia de concavidad. Es decir, pasa de ser cóncavo a ser convexo , o viceversa.

Optimización

La optimización es una aplicación directa del cálculo diferencial y sirve para calcular máximos y mínimos de funciones sujetas a determinadas condiciones. La aplicación práctica de los problemas de optimización es bien clara: calcular superficies o volúmenes máximos, costes mínimos, forma óptima de determinadas figuras...

Es importante en este tipo de problemas identificar claramente la función a optimizar que suele depender de dos variables. El ejercicio nos dará una condición que liga a ambas y lo que debemos hacer es despejar una de ellas y sustituirla en la función a optimizar, de forma que tengamos una sola variable. A partir de aquí aplicaremos la teoría del cálculo diferencial para identificar máximos o mínimos.

En la resolución de problemas de optimización de funciones seguiremos los siguientes pasos:

1.  Plantear la función que hay que maximizar o minimizar.

2.  Plantear una ecuación que relacione las distintas variables del problema, en el caso de que haya más de una variable.

3.  Despejar una variable de la ecuación y sustituirla en la función de modo que nos quede una sola variable.

4.  Derivar la función e igualarla a cero, para hallar los extremos locales.

5.  Realizar la 2ª derivada para comprobar el resultado obtenido.

GRACIAS!!!💓